
DefinitionĪ recurrence relation is an equation that recursively defines a sequence where the next term is a function of the previous terms (Expressing $F_n$ as some combination of $F_i$ with $i < n$). Finally, we introduce generating functions for solving recurrence relations. The general approach is to transform an equation to a previously. We study the theory of linear recurrence relations and their solutions. In mathematics, a recurrence relation is an equation that recursively defines a sequence. The procedure for finding the terms of a sequence in a recursive manner is called recurrence relation. I have explicit form of arithmetic sequence h(n) 1 + 4n h ( n) 1 + 4 n where I have to convert it to recursive form to find the first term and the common difference. What is a fibonacci Sequence A Fibonacci sequence. This process is recursive so dependencies of dependencies (and so on) will also. 23) a 21 1.4, d 0.6 24) a 22 44, d 2 25) a 18 27.4, d 1.1 26) a 12 28.6, d 1.8 Given two terms in an arithmetic sequence find the recursive formula. The formula for the nth term of a Fibonacci sequence is an a(n-1) + a(n-2), where a1 1 and a2 1. This context is an explicit object in JS and Go but is implicit with the CLI.


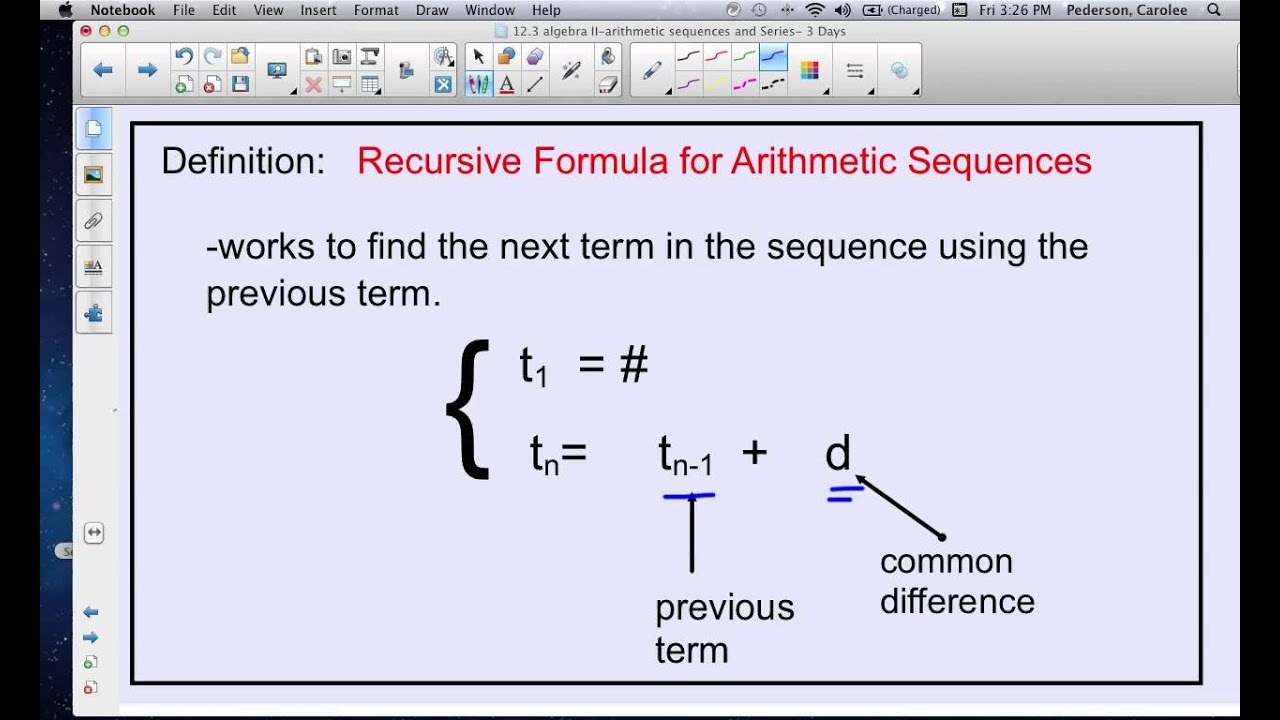
In this chapter, we will discuss how recursive techniques can derive sequences and be used for solving counting problems. Given a term in an arithmetic sequence and the common difference find the recursive formula and the three terms in the sequence after the last one given.


 0 kommentar(er)
0 kommentar(er)
